Research Contributions
Words ‘competition’, ‘collaboration’ and ‘connection’ are often associated with human behavior and interactions. My past and ongoing research directions focus on these phenomena occurring in quantum materials deciding their complex behavior.
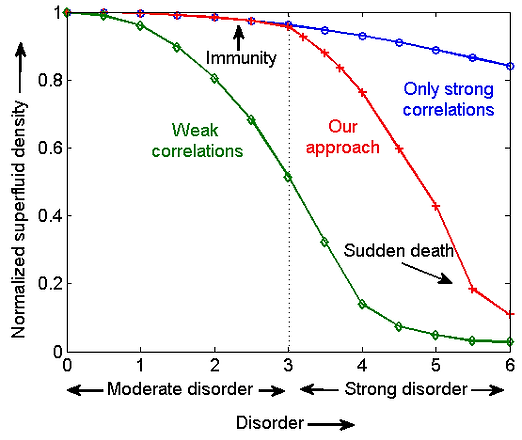
Competition and collaboration between disorder and strong electronic correlations
In my doctoral studies, I focused on the competition between two phenomena - disorder and strong electronic interactions in d-wave superconductors with a primary emphasis on materials like high-temperature cuprate (copper-oxide based) superconductors. The repulsive electron-electron interactions are known to be significant for cuprates as they turn the undoped half-filled compounds into an insulator. This is quite different from the metallic non-superconducting state of a standard isotropic superconductor. These interactions tend to smear out any charge accumulation by prohibiting the formation of double occupancy of electrons on any lattice site especially when they are strong. On the other hand, disorder, which is intrinsic to doped cuprates, tries to localize the electrons in space, leading to a complex interplay. Typically, d-wave superconductivity is believed to be extremely sensitive to impurities because of the anisotropic gap structure. So, we ask the following question: Can the strong electronic correlations modify this conventional wisdom of an easy destruction of the anisotropic d-wave superconductivity in the cuprates by impurities? In search of the answer, we, for the first time, have formulated a unified theoretical approach where strong correlations compete with moderate disorder to keep superconductivity ‘immune’ and collaborate with strong disorder resulting in ‘sudden death’ of superconductivity. For reference see our works New J. Phys. 16, 103018 (2014), Phys. Rev. B 95, 014516 (2017) and Phys. Rev. B 96, 134518 (2017).
Competition and connection between superconductivity and charge density wave
In my post-doctoral tenure, I turned my attention to a different form of competition; a competition between two electronic phases again in the context of cuprates. Electrons often join hands due to mutual interactions to form cooperative states with different physical properties, e.g., superconductivity and periodic modulations of charge or spin. If these phases compete for the same conduction electrons, they tend to suppress each other. Similar competition is seen in the cuprates, where the investigation of a non-superconducting phase at low temperatures is hindered by the presence of robust superconductivity. The application of an external magnetic field suppresses superconductivity and other ‘novel’ electronic phases appear. Thus the phase diagram of cuprates in the applied magnetic field (B) - temperature (T) plane can enlighten us with some key aspects of these materials including the mysterious pseudogap phase. Several experiments indicate that the charge density wave order competes with the superconductivity in the pseudogap phase of cuprates. On the other hand, there are proposals that the charge order is related to the superconductivity by an emergent symmetry. We have described various features of the experimentally observed B-T phase diagram of cuprates at different dopings using both a Ginzburg Landau theory of competing orders and an emergent SU(2) picture where there is an intimate connection between the two orders. For reference see our work Phys. Rev. B 97, 214501 (2018) and one of my talks.
Sign-problem free quantum Monte Carlo
The main hindrance in the full understanding of the collective behavior of interacting fermions is the limited availability of exact analytical results. On top of it, the famous "fermion sign-problem" restricts their investigation even numerically in Monte Carlo methods. But there are some special cases where the quantum Monte Carlo simulations can be sign-problem free. One such example is a spin fermion model with two bands mimicking some features of the fermiology of the cuprates. As a part of an ongoing project, I am currently developing a determinant quantum Monte Carlo code for this model in order to study various instabilities arising out of spin fluctuations.
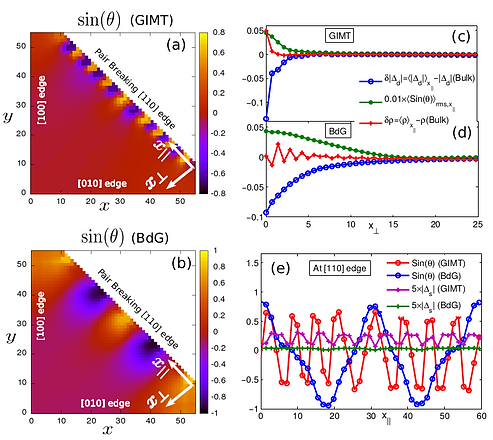
Interplay of strong correlations, topology, and disorder in high-temperature superconductors
My past research has inspired me to look at a scenario where disorder and various non-superconducting broken symmetry orders interfere with a third player, topology. In this direction, in my second postdoc, we realized that studying a pair breaking (110) edge (an edge perpendicular to x=y line in the crystallographic plane) of a cuprate superconductor can be very prospectus direction since this is an archetype example where strong correlations, topology, and disorder are always strongly intertwined. These edges host a flat band of topological zero-energy states. Due to the thermodynamic instability of these zero-energy states, spontaneous symmetry breaking can occur, where the topological protection is broken to lower the energy cost. One exotic possibility is a “phase crystal”, where the phase of the d-wave order parameter develops a periodic modulation, breaking both time-reversal and translational symmetries along the edge. We have shown that the strong interactions give rise to a new phase of matter where the phase crystals accompany a modulating extended s-wave order and hence develop a full gap. This fully gapped phase crystal state is unexpectedly robust to omnipresent disorder, but only due to the presence of strong interactions. Through this exercise, we have shown how the combined effect of strong interactions, topology, and disorder generates rich physics that defies the conventional expectations when these effects are considered separately. For reference see our work npj Quantum Materials 7, 44 (2022)
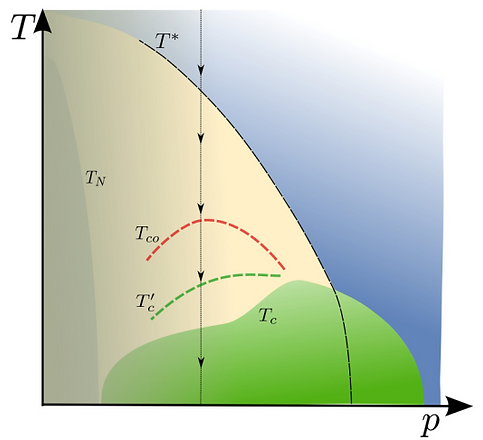
Fractionalized Cooper pair density waves in underdoped cuprates
The pseudogap phase of underdoped cuprates remain a mystery till date. To understand the mysterious pseudogap, we have development a theory that finds a unique underlying reason for the origin of the pseudo-gap phase by showing that the competition between charge density waves and superconducting order comes from fractionalization of a Cooper pair density wave order parameter. Using this theory, we have been successful in explaining the Fermi arcs seen in angle-resolved photoemission spectroscopy and also other unexplained features of these experiments. In addition, we have been successful in explaining various experimental puzzles within this theory. For reference see our work Phys. Rev. B 100, 224511 (2019).
Odd-frequency superconductivity
Cooper pairs are the basic building blocks of superconductivity. One unknown and highly mysterious forms of Cooper pairs are odd-frequency Cooper pairs which are not the usual Bardeen-Cooper-Schrieffer (BCS) equal time Cooper pairs, but unequal time Cooper pairs. One remarkable application of the presence of odd-frequency Cooper pairs is the dissipation-less spin transport in superconductor-ferromagnet junctions, with potential of revolutionizing the field of superconducting spintronics We identified that the odd-frequency Cooper pairs necessarily need electrons of different energy to pair. We have investigated the fate of these finite energy pairs when they intertwine with finite momentum pairs. One of the main challenges in the field of odd-frequency superconductivity is the lack of its direct experimental evidence. We have postulated that the quantum interference patterns generated in a superconductor due to the omnipresence of impurities have distinct features due to the time, or equivalently frequency symmetry of Cooper pairs. In particular, we have shown that a commonly used experimental tool namely scanning tunneling microscopy can be used to directly detect the time symmetry of Cooper pairs. For reference see our works Phys. Rev. Lett. 129, 247001 (2022), Editor's suggestion, featured in Physics; Phys. Rev. B. 106 , 024511 (2022); New J. Phys. 23 , 033001 (2021).
Superconductivity in altermagnets
Magnetism and superconductivity are the two most celebrated quantum phases of matter. These two phases share a "friend-foe" dichotomous relation. While ferromagnetism is believed to be a foe to spin-singlet superconductivity, proximity to antiferromagnetism can give rise to unconventional spin-singlet superconductivity. Very recently a third form of magnetism has been discovered, namely altermagnetism. Altermagnets has unconventional nature with distinct symmetry properties compared to the other two known forms, ferromagnetism and antiferromagnetism, apart from having some shared similarities to both. On one side, similar to ferromagnets, altermagnets break time-reversal symmetry due to broken Kramers spin degeneracy. On the other side, similar to antiferromagnets, the net magnetization in altermagnets is zero due to sign changing values. This brings in a fundamental question: can spin-singlet superconductivity show up in altermagnets? An answer to this question can open a new avenue of research in condensed matter physics. We address this question by investigating the possibility of spin-singlet superconductivity in altermagnets, particularly focusing on unconventional superconductivity. Due to the unconventional nature of both altermagnets and superconductivity, we find finite-momentum superconductivity even when the net magnetization is zero in altermagnets. This finding gives an altermagnetic route to long-sought after finite-momentum superconductivity and can perhaps give possible explanation to the origin of pair density waves observed in cuprate superconductors which in the undoped state are shown to be altermagnets. In the additional presence of external magnetic field, we find a never-before-seen phase diagram looking like a “Yoda-ear”. We predict that applying magnetic field can induce unconventional superconductivity in altermagnets, providing guidance for its future experimental discovery. For reference see our work arXiv:2309.14427 (2023).
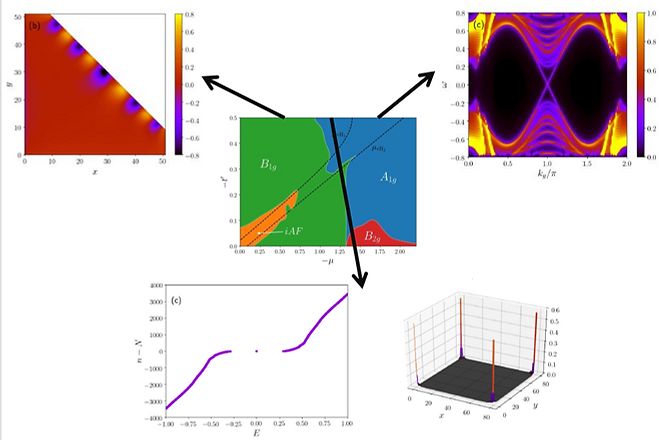
Topological superconductivity as a quantum phase of matter
Topological superconductors are of high current interest due to their exceptional properties and potential for applications in quantum information technologies. These can be of two different types (i) Engineered heterostructures in which topological superconductivity is proximity induced by a conventional s-wave superconductor and (ii) intrinsic topological supercondcutors which arise as an intrinsic property of the material. Intrinsic topological superconductors have several advantages compared to their engineered counterparts: For one, they exhibit higher transition temperatures and are less affected by impurities. Moreover, their topological superconductivity exists in the entire volume of the material, and not just at a heterostructure interface. We have shown that the combined effects of van Hove singularities, Rashba spin-orbit coupling, and repulsive Hubbard interactions give rise to a cascade of topological superconducting states, including a nodal d-wave state with flat-band Majorana edge modes, a fully gapped p-wave state with helical Majorana edge modes, and a time-reversal breaking d+ip state with Majorana corner modes. While the first two pairing states have first order topology, characterized by a winding number and a Pfaffian invariant, respectively, the third one exhibits higher-order topology. For reference see our work arXiv:2304.07100 (2023).